Graphs Gallery

Here are several interesting graphs plotted with Advanced Grapher.

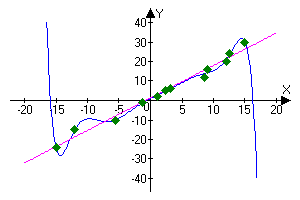
Regression Regression
The equations of curves are obtained with the help of the regression analysis of the tabular data (which are shown by points)
Y(x)=-(1.1100319*10^(-8))*x^9 + (4.2010685*10^(-8))*x^8 + (4.8204417*10^(-6))*x^7 - (1.9123759*10^(-5))*x^6 - (6.0569249*10^(-4))*x^5 + 0.0026407*x^4 + 0.0193816*x^3 - 0.0956714*x^2 + 1.6439131*x + 1.0095675 (polynomial regression, polynomial power is 9)
Y(x)=1.665949*x+1.3004023 (linear regression)
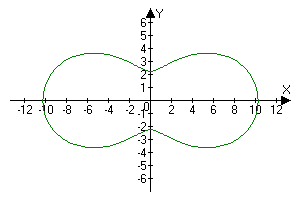
Cassini curve Cassini curve
R(a)=2^2*cos(2*a)+sqrt(2.5^4-2^4*sin(2*a)^2)
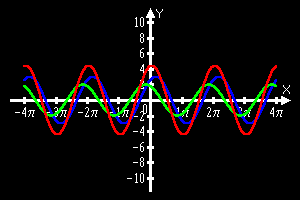
Addition of oscillations Addition of oscillations
Y(x)=sin(x+1)*3
Y(x)=sin(x+2)*2
Y(x)=sin(x+1)*3+sin(x+2)*2
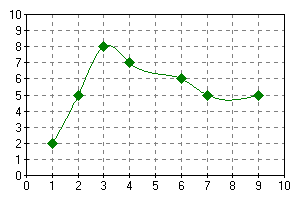
Smoothing Smoothing
Table: 7 items
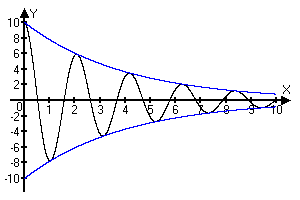
Damped oscillations Damped oscillations
Y(x)=exp(-x/4)*10*cos(x*3)
Y(x)=exp(-x/4)*10
Y(x)=-exp(-x/4)*10
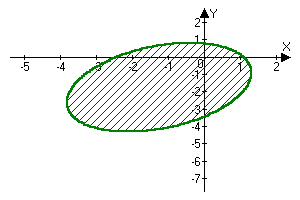
Ellipse Ellipse
3*x*x-2*x*y+x*4+y*8+3*y*y-8<0
3*x*x-2*x*y+x*4+y*8+3*y*y-8=0
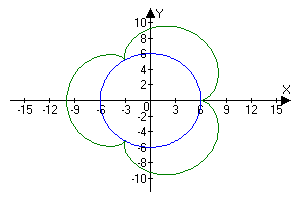
Epicycloid Epicycloid
X(t)=(6+2)*cos(t)-2*cos((6+2)/2*t);
  Y(t)=(6+2)*sin(t)-2*sin((6+2)/2*t)
R(a)=6
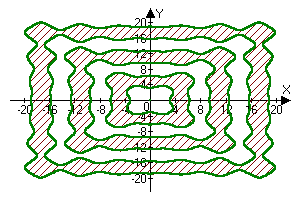
Equation and inequality Equation and inequality
x*sin(x)+y*sin(y)<0
x*sin(x)+y*sin(y)=0
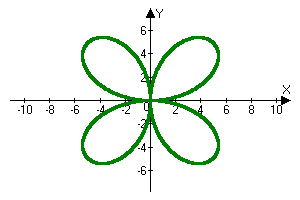
Four-leaved rose Four-leaved rose
R(a)=7*sin(2*a)
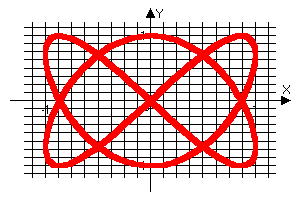
Ortogonal oscillations Ortogonal oscillations
X(t)=sin(2*t); Y(t)=sin(3*t)
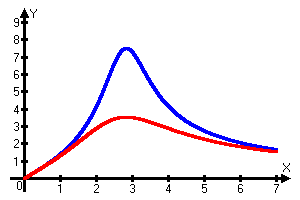
Resonance Resonance
Y(x)=15/sqrt(4+(1.5*x-12/x)^2)
Y(x)=15/sqrt(18+(1.5*x-12/x)^2)
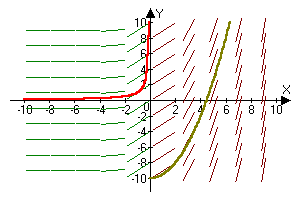
Slope fields Slope fields
dy/dx=1/x^2
 dy/dx=x
 Y(x)=-1/x
 Y(x)=x*x/2-10
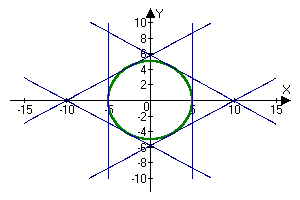
Tangents Tangents
 The equations of the tangents are obtained with the help of this program
R(a)=5
 X(y)=5
Y(x)=-0.5913984*x+5.8089414
Y(x)=0.5773502*x+5.7735026
X(y)=-5
Y(x)=-0.5773504*x-5.773503
Y(x)=0.5773504*x-5.773503
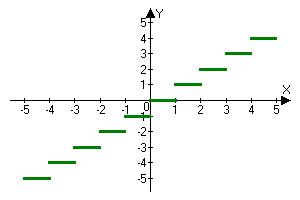
Integer part Integer part
 Y(x)=int(x)