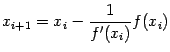Вперед: Метод хорд (метод линейной интерполяции) Наверх: Приближённое нахождение корней уравнений Назад: Метод одной касательной  

Метод Ньютона (метод касательных)

Рассмотрение предыдущего метода позволяет предположить, что итерации станут приближаться к корню ещё быстрее, если мы будем выбирать касательную вместо секущей не только на первом, а на каждом шаге. Ясно, что тогда формула итераций будет иметь вид

$\displaystyle x_{i+1}=x_i-\dfrac{1}{f'(x_i)}f(x_i)$ (9.1)

(сравните с формулой метода одной касательной). Этот метод называется методом касательных, или методом Ньютона. Действительно, последовательные приближения метода Ньютона сходятся гораздо быстрее, чем в общем методе итераций (скорость сходимости приближений в котором, напомним, та же, что у геометрической прогрессии со знаменателем $ {\gamma}$ при $ 0<{\gamma}<1$).

Поскольку для метода Ньютона

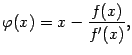
$\displaystyle {\varphi}(x)=x-\dfrac{f(x)}{f'(x)},$

то

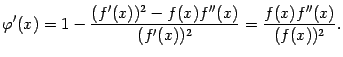
$\displaystyle {\varphi}'(x)=1-\dfrac{(f'(x))^2-f(x)f''(x)}{(f'(x))^2}= \dfrac{f(x)f''(x)}{(f(x))^2}.$

В точке $ x^*$ получаем $ {\varphi}'(x^*)=0$, так как $ f(x^*)=0$. Тем самым, в этом методе график $ y={\varphi}(x)$ пересекает прямую $ y=x$ в точности по горизонтали, что приводит к очень быстрой сходимости итераций к $ x^*$. Именно, имеет место оценка

$\displaystyle \vert x_{i+1}-x^*\vert\leqslant c\vert x_i-x^*\vert^2\leqslant \dfrac{1}{c}(c\vert x_0-x^*\vert)^{2^{i+1}},$ (9.2)

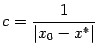где $ c$ -- некоторая постоянная (не зависящая от $ i$). Если начальное приближение $ x_0$ взято достаточно близко от корня $ x^*$, то можно взять $ c=\dfrac{1}{\vert x_0-x^*\vert}$.

Заметим, что по сравнению с общей оценкой метода итераций

$\displaystyle \vert x_{i+1}-x^*\vert\leqslant {\gamma}\vert x_i-x^*\vert,$

постоянная $ {\gamma}<1$ заменяется в оценке метода Ньютона (9.2) на стремящуюся к 0 величину $ c\vert x_i-x^*\vert$; отсюда и высокая скорость сходимости.

Доказательство оценки (9.2) можно найти в учебниках, специально посвящённых численным методам, например, [Амосов А. А., Дубинский Ю. А., Копченова Н. В. Вычислительные методы для инженеров. -- М.: Высш. шк., 1994], [Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. -- М.: Наука, 1987], [Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. -- М.: Наука, 1986].

Скорость сходимости итераций, которая задаётся формулой (9.2), называется квадратичной. Квадратичная скорость сходимости означает, примерно говоря, что число верных знаков в приближённом значении $ x_i$ удваивается с каждой итерацией. Действительно, если $ c\approx1$, и $ \vert x_i-x^*\vert\approx10^{-n}$, то $ \vert x_{i+1}-x^*\vert\approx10^{-2n}$. Это и означает, что число верных знаков при переходе к следующему приближению возросло с $ n$ до $ 2n$, то есть удвоилось.

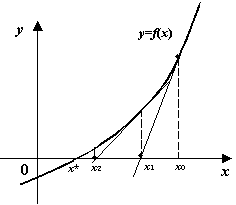
Геометрический смысл метода Ньютона состоит в том, что на каждом шаге мы строим касательную к графику $ y=f(x)$ в точке очередного последовательного приближения $ x_i$, а за следующее приближение $ x_{i+1}$ берём точку пересечения этой касательной с осью $ Ox$. Тем самым наклон прямой подстраивается на каждом шаге наилучшим образом (ведь кривизну графика, связанную с второй производной, мы не учитываем, и поэтому неизвестно, в какую сторону от касательной отклонится график).

Рис.9.13.Последовательные приближения метода Ньютона


Заметим, что по-другому идею метода Ньютона мы можем описать так: на каждом шаге вместо исходного уравнения $ f(x)=0$ мы решаем приближённое, линеаризованное в точке $ x_i$ уравнение

$\displaystyle f(x_i)+f'(x_i)(x-x_i)=0,$

в котором левая часть -- это многочлен Тейлора первого порядка для функции $ f(x)$ в точке $ x_i$, то есть линейная функция

$\displaystyle \ell_{x_i}(x)=f(x_i)+f'(x_i)(x-x_i).$

Решением линеаризованного уравнения $ \ell_{x_i}(x)=0$ служит следующее приближение $ x_{i+1}$, в то время как решением исходного точного уравнения $ f(x)=0$ служит искомый корень $ x^*$.

Идея замены точной (но сложной) задачи последовательностью более простых линеаризованных задач весьма продуктивна в приближённых методах; например, такая идея даёт эффективный способ решения многомерных задач с ограничениями (метод Франка - Вулфа в нелинейном программировании, см., например, [Киселёв В.Ю., Экономико-математические методы и модели. -- Иваново: изд. ИГЭУ, 1998]).

        Пример 9.7   Решим методом Ньютона всё то же уравнение $ x^3+2x^2+3x+5=0$, взяв в качестве начального приближения $ x_0=-2$ и задав точность $ {\varepsilon}=0.000001$ (ту же, что была взята при решении этого уравнения методом одной касательной). Поскольку $ f'(x)=3x^2+4x+3$, то итерационная формула метода Ньютона будет такой:

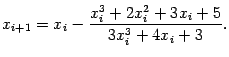
$\displaystyle x_{i+1}=x_i-\dfrac{x_i^3+2x_i^2+3x_i+5}{3x_i^3+4x_i+3}.$

Применяя эту формулу, последовательно находим:

$\displaystyle x_1=-1.857143;x_2=-1.843842;x_3=-1.843734;x_4=-1.843734,$

так что $ \wt x=-1.843734$ с точностью $ {\varepsilon}$. Как мы видим, значение корня с нужной нам точностью было получено уже на третьем шаге. (Четвёртый шаг понадобился для того, чтобы можно было убедиться, что с нужной нам точностью значение перестало изменяться.)     

        Упражнение 9.2   Найдите тот же корень, начав с $ x_0=-1$. (Заметим, что итерационную формулу при этом менять не надо, в отличие от метода одной касательной.) Сколько потребуется итераций для достижения той же точности? Обратите внимание на то, что сначала приближения ($ x_1$ и $ x_2$) окажутся даже вне отрезка $ [-2;-1]$, но затем $ x_i$ быстро сходятся к $ x^*$ с той же стороны, что в примере.

Ответ: Потребуется 6 итераций.     


Вперед: Метод хорд (метод линейной интерполяции) Наверх: Приближённое нахождение корней уравнений Назад: Метод одной касательной